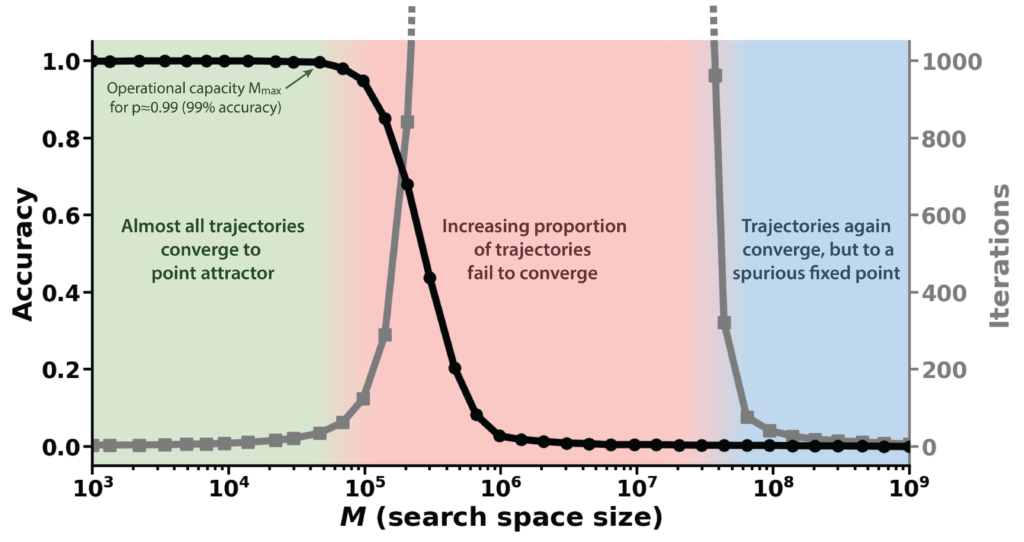
An exciting new model of factorization in neural circuits, called resonator networks, has been published in the December issue of Neural Computation. Appearing as a two-part series, the articles by Paxon Frady, Spencer Kent, and collaborators, detail how factorization problems arise in cognition and how resonator networks may be a powerful new tool for solving such problems efficiently. They explain how resonator networks define a nonlinear dynamical system with fascinating properties and how using this system to solve an important vector factorization problem is superior to a number of alternative approaches. This opens the door for applications of Vector Symbolic Architectures (VSAs, otherwise known as HD Computing) to a much wider range of problems than previously considered, and is a cornerstone of our ongoing efforts to explore VSAs as framework for cognitive representation in the brain. You can view both articles by visiting our publications page.